|
Accueil de la bibliothèque > La musique et les musiciens
LA MUSIQUE ET LES MUSICIENS - CHAPITRE PREMIER - Étude du son musical - Production du son - Sons harmoniques > CHAPITRE PREMIER - Étude du son musical > Production du son - Sons harmoniques Cette fois, le chevalet et les poids sont inutiles; au moyen des chevilles,
mettons l'instrument dans le ton d'ut
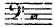 , qui correspond à 258 vibrations et 6 dixièmes.
La corde, attaquée vers son milieu avec l'archet, prend nécessairement pour
vibrer une forme en fuseau, qu'on peut se représenter ainsi (fig. 8) : , qui correspond à 258 vibrations et 6 dixièmes.
La corde, attaquée vers son milieu avec l'archet, prend nécessairement pour
vibrer une forme en fuseau, qu'on peut se représenter ainsi (fig. 8) :
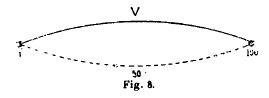
et fait entendre le son fondamental que nous connaissons déjà, et que noue
appellerons ici son partiel 1. Aux deux
extrémités fixes, le mouvement est nécessairement nul, le point milieu, où la
vibration a sa plus grande amplitude, est un ventre.
Avec un doigt de la main gauche, ou simplement avec une barbe de plume, opérons
un très léger contact sur ce point central, juste assez pour empêcher le ventre
de s'y former, et attaquons avec l'archet vers le centimètre 25; un nouveau
point immobile, qu'on appelle un nœud, se formera sous notre doigt, et la corde
vibrera selon cette figure (fig. 9) :
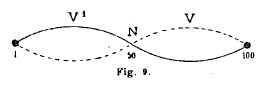
Il y aura donc un nœud et deux ventres; chacun des segments vibrants, n'étant
plus que d'une moitié de la corde, opérera un nombre double de vibrations, soit
517,2, et le
son produit sera à l'octave du précédent :
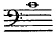 . C'est ce
qu'on appelle le deuxième harmonique, ou son 2. . C'est ce
qu'on appelle le deuxième harmonique, ou son 2.
Procédant de la même manière, effleurons la corde au centimètre 33,
ébranlons-la au centimètre 50, et nous entendrons le 3e harmonique ou
son 3 : 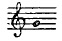 . Le nombre
des vibrations sera 775, et la corde aura pris cette nouvelle formé (fig. 10) : . Le nombre
des vibrations sera 775, et la corde aura pris cette nouvelle formé (fig. 10) :
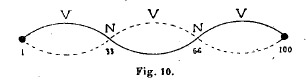
Il est à observer ici qu'en outre du nœud que nous
provoquons par le contact, il s'en est formé spontanément on autre au point 66;
ce fait est facile à constater en promenant successivement l'archet sur chacun
des trois ventres (centimètres 16, 50 et 82 approximativement); le son 3 sortira
nettement. Au contraire, si on touche avec l'archet au point 66, qui doit rester
immobile, l'harmonique ne se produit plus.
On trouvera le son 4
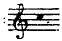 qui correspond nécessairement à 1,034,5 vibrations et à la forme (fig. 11) : qui correspond nécessairement à 1,034,5 vibrations et à la forme (fig. 11) :
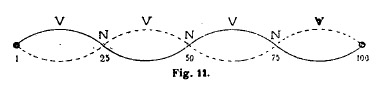
en effleurant au point 25 et en ébranlant vers 12, 37, 62 ou 87, c'est-à-dire
sur les ventres; ici deux noeuds se sont formés spontanément.
Il est facile de produire ainsi sur le monocorde, surtout en se servant d'une
corde fine, les dix premiers harmoniques, dont voici le tableau, avec
l'indication du point à effleurer (premier nœud), et le nombre de vibrations de
chaque son, qui n"est autre que le premier chiffre multiplié par le n° d'ordre
de chaque son partiel.

Théoriquement, la série des harmoniques peut être considérée comme infinie,
puisque la corde peut être indéfiniment divisée; mais pour ce qui nous occupe, les dix premiers sont suffisants.
Cette série donne lieu aux remarques suivantes, qui méritent de fixer
l'attention :
1° Les numéros d'ordre sont égaux aux nombres de segments vibrants, ou de
ventres ;
2° Il y a toujours un nœud de moins que de ventres ;
3° Le son fondamental, ne formant qu'un seul ventre, doit être considéré comme
son propre 1er harmonique1.
4° Pris dans leur ordre numérique, les harmoniques vont toujours en se
rapprochant, et forment successivement des intervalles d'octave, de quinte,
quarte, tierce et seconde.
5° Les harmoniques 1, 2, 4, 8 sont en rapport d'octave. (Si on poursuivait la
série, il en serait de même des harmoniques 16, 32, 64, etc.) Ce même rapport
d'octave se retrouve entre 3 et 6, et entre 5 et 10.
6° Les nombres relatifs de vibrations, pour deux sons en rapport
| d'octave sont comme |
1: 2, |
| de quinte juste sont comme |
2:3, |
| de quarte juste sont comme |
3:4, |
| de tierce majeure sont comme |
4:5, |
| de tierce mineure sont comme |
5:6, |
| de seconde majeure sont comme |
8:9. |
7° Enfin, on obtient le nombre de vibrations d'un
harmonique quelconque en multipliant par son numéro d'ordre le nombre de
vibrations du son fondamental.
1. Certains théoriciens ont numéroté autrement les sons harmoniques ; pour eux,
le son fondamental ne compte pas; ce serait le son zéro; ils appellent l'octave
première harmonique; la douzième, deuxième, etc.
Le système adopté ici est celui de tous les grands physiciens actuels ; il est
incomparablement plus commode pour le calcul, comme on le verra dans les
paragraphes suivants.
|

