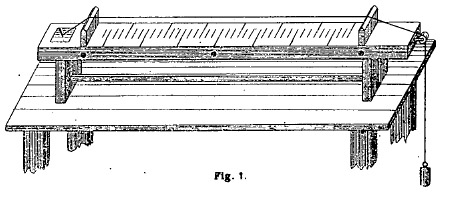
Cet instrument s'appelle le monocorde, et consiste simplement en une longue caisse rectangulaire étroite, sur laquelle une corde est tendue au moyen, soit de deux chevilles, soit d'une cheville fixe et d'un poids que l'on peut faire varier. La corde a un mètre de longueur, et au-dessous d'elle se trouve inscrite sur la table la division de mètre en décimètres, centimètres et millimètres. Cet instrument est complété par un chevalet mobile avec lequel on délimite à volonté la portion de la corde sar laquelle on veut expérimenter (fig. 7).

Voici quelques exemples des innombrables et instructives expériences que l'on peut faire avec ce simple appareil, qui se trouve dans tous les cabinets de physique.

Après l'avoir accordée dans un ton quelconque, ébranlez la corde, soit avec un archet, soit en la pinçant avec le doigt, soit en la frappant; vous entendrez ainsi le son qu'elle produit en vibrant dans toute sa longueur, un mètre; placez alors le chevalet mobile juste au milieu, à 50 centimètres, et de quelque côté que vous ébranliez la corde, elle produira un son exactement à l'octave aiguë du premier. Cela démontre que les nombres de vibrations des cordes sont en raison inverse de leurs longueurs.

Remplacez cette corde par une autre, de même substance, dont le diamètre soit exactement double de celui de la première; donnez-lui la même tension, c'est-à-dire employez pour la tendre les mêmes poids, et vous obtiendrez l'octave inférieure. Cela démontre que les nombres de vibrations des cordes sont en raison inverse de leurs diamètres.

En expérimentant successivement sur deux cordes de même diamètre et soumises à la même tension, mais formées de métaux différents, on arrive à trouver que les nombres de vibrations des cordes sont en raison inverse des racines carrées des densités.

De même, en faisant varier dans les rapports convenables les poids tenseurs, il est facile de constater que les nombres de vibrations des cordes sont en raison directe de la racine carrée du poids par lequel elles sont tendues.

Ces quatre lois fondamentales, dont la connaissance approfondie est nécessaire pour les constructeurs d'instruments, peuvent être ainsi résumées à l'usage des musiciens :

Plus une corde est longue, grosse, lourde et faiblement tendue, plus ses vibrations sont lentes, et plus par conséquent le son est grave ;

Plus elle est courte, fine, légère et fortement tendue, plus ses vibrations sont rapides, et plus par conséquent le son est aigu.

Le son ainsi produit par une corde vibrant dans toute sa longueur s'appelle son fondamental ou son naturel, mais elle est apte à fournir aussi beaucoup d'autres sons, en se subdivisant pour vibrer; on les appelle sons harmoniques¹, et, pour les étudier, nous allons avoir de nouveau recours à notre monocorde.

1. On dit aussi, dans le même sens : sons concomitants, hypertons, (all. obertone = sons supérieurs), ou encore sons partiels.