Accueil de la bibliothèque > La musique et les musiciens > CHAPITRE PREMIER - Étude du son musical > Rapports des sons simultanés. Intervalles; accords; consonance et dissonance.

E. — Rapports des sons simultanés. Intervalles; accords; consonance et dissonance.

Nous arrivons aux combinaisons simultanées des sons, aux accords, c'est-à-dire au principe même de la consonance et de la dissonance. Il est facile de prévoir que l'explication s'en trouve dans le phénomène même de la production du son, avec son accompagnement naturel d'harmoniques, et que la clef nous en sera livrée par le monocorde, qui aura été ainsi, du commencement à la fin, l'instrument de nos investigations.

L'idéal de la consonance, ce serait le son rigoureusement pur, dégagé de tout alliage de sons partiels ; de tels sons, nous l'avons déjà dit, n'existent que théoriquement, mais pourtant le diapason, quelques notes de flûte, certains tuyaux d'orgue (dits jeux de flûte), peuvent nous donner l'idée d'un son presque simple. En dehors de cette consonance idéale, tout son est un son complexe ; mais il se rapproche d'autant plus de la pureté théorique que les harmoniques qui le composent sont en rapport numérique plus simple avec lui-même. Plus les sons partiels sont proches du son principal, mieux ils lui font cortège, et mieux aussi ils l'accompagnent et produisent sur notre organisation la sensation agréable que nous qualifions de consonance. Si, au contraire, les sons partiels sont très éloignés de leur son fondamental, et par conséquent très rapprochés entre eux, nous n'avons plus la perception d'un tout homogène, mais d'un son pauvre en lui-même, accompagné d'un bruit aigu désagréable ; c'est la dissonance. Il en est absolument de même pour les agrégations de sons qu'on nomme accords, et dans lesquelles l'art ne fait qu'imiter la nature. Plus on se rapproche, dans ces groupements, du son simple théorique, et plus le résultat obtenu est consonant, dans le sens musical du mot.

En réalité, la limite absolue entre la consonance et la dissonance n'existe pas ; elle varie selon le degré de sensibilité de l'ouïe chez chaque individu, et aussi selon l'accoutumance résultant de l'éducation; c'est une question de tolérance de l'oreille, ce qui est dur pour l'un pouvant paraître très agréable à son voisin. On n'en peut pas plus discuter que des goûts et des couleurs.

Mais, s'il est impossible de dire où finit la consonance et où commence la dissonance, il est très facile au contraire d'établir une gradation, en laissant chacun libre de mettre la barrière là où il lui plaira.

C'est ce que nous allons faire, en reprenant le monocorde et en étudiant de nouveau la série des harmoniques, source inépuisable d'où dérive, en somme, tout le matériel de l'art musical. Cette fois, je présente les harmoniques de do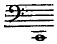en les reliant deux par deux et consécutivement de façon à en tirer tous les groupes offrant des rapports différents.

Étant donné que l'idéal de la consonance, la pureté absolue, serait exprimé par le rapport 1/1, qui est effectivement celui de l'unisson, il est certain que plus nous en approchons, c'est-à-dire plus le rapport est simple, et plus il y a consonance; en lisant les fractions de l'exemple ci-dessus dans l'ordre où elles se présentent, nous trouvons donc une série de groupes de deux sons de moins en moins consonants, de plus en plus dissonants.