Reprenons la gamme majeure et envisageons-la sous une nouvelle face, plus familière aux musiciens. Les sons dont elle se compose, et dont nous avons démontré l'affinité, la parenté plus on moins directe avec un son principal appelé tonique, sont inégalement espacés entre eus. Ils présentent cinq intervalles à peu près semblables, et deux autres sensiblement plus petits; ce sont les tons et les demi-tons, ainsi distribués :

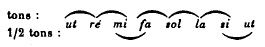
Ces deux demi-tons admis, il est naturel que les musiciens, toujours désireux d'enrichir leur système par l'addition de nouveaux sons, aient songé à en intercaler d'autres dans les cinq grands espaces, de façon à obtenir une suite discontinue de demi-tons. Mais encore fallait-il, pour satisfaire leur oreille, que ces sons nouveaux fussent choisis de telle façon qu'il existât un lien quelconque entre eux et la tonique. Ce lien, voici la manière ingénieuse dont Barbereau en démontrait l'existence :
Les sept notes de la gamme naturelle, rangées dans un certain ordre, présentent une série de quintes justes :
    fa do sol ré la mi si

Si on poursuit cette série (toujours par quintes justes), à droite, on obtient cinq nouveaux sons :

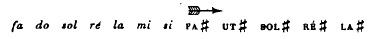
qui, intercalés avec les premiers, viennent justement remplir les espaces de tons, ainsi :

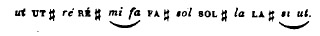
Si on prolonge au contraire la série à gauche :

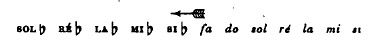
les mêmes espaces sont également remplis, mais cette fois au moyen des bémols :

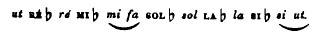
Ces deux séries, celle par dièses et celle par bémols, nous offrent chacune une succession de quintes absolument justes, de quintes pythagoriciennes¹, du rapport exact 3/2. Si l'on compare entre eux les sons intercalaires correspondants, au moyen du calcul, on trouve qu'ils diffèrent par la faible quantité appelée comma², qui approche tellement de la limite d'appréciation des sons, que, tout en reconnaissant mathématiquement son existence, on peut musicalement la considérer comme négligeable. Il existe à ce sujet une singulière divergence entre les musiciens et les physiciens : ces derniers, se basant sur des calculs positifs, veulent absolument que l'ut dièse soit plus bas que le ré bémol, tandis que les musiciens, guidés par leur sens artistique, affirment énergiquement le contraire. Toujours est-il que, par des concessions réciproques, justifiées par la tolérance de l'oreille, on a admis que ut# = réb (puis, par extension aux autres sons intercalaires, ré# = mib, fa# = solb, sol# = lab, la# = sib), ce qui a constitué la seule vraie gamme chromatique réellement pratique, dite gamme tempérée:

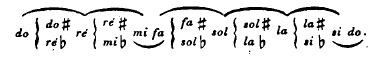
Cette gamme est formée de douze sons espacés symétriquement, parmi lesquels se retrouvent ceux de la gamme diatonique, au nombre de sept, plus cinq autres, qui portent chacun deux noms différents, restés nécessaires au point de vue de l'orthographe musicale, ce qui les a fait appeler notes synonymes. Aucun d'eux n'est rigoureusement juste, mais il s'en faut de si peu que l'oreille la plus délicate n'y trouve rien qui la choque³.

Tel est, avec ses défauts et ses qualités, le système de tonalité accepté de nos jours dans les pays les plus avancés en civilisation. On l'appelle tempérament. C'est ainsi que sont accordés les pianos, les orgues, tous les instruments à sons fixes. Les instruments à cordes, les voix, et dans certains cas les instruments à vent, possèdent la faculté de faire différer les notes synonymes.

1. Voir plus loin Histoire de la musique.
2. Les musiciens disent que le comma est la neuvième partie du ton. Pour les physicien», c'est le rapport 81/80. Le comma pythagoricien est 531441/524288.
3. La valeur déjà si faible du comma pythagoricien 531441/524288 se trouve répartie par douzième sur chacune des douze quintes.