|
Accueil de la bibliothèque > La musique et les musiciens
LA MUSIQUE ET LES MUSICIENS - CHAPITRE PREMIER - Étude du son musical - Rapports des sons successifs. Tonalité. - Notes tonales > CHAPITRE PREMIER - Étude du son musical > Rapports des sons successifs. Tonalité. - Notes tonales Abstraction faite des timbres, qui n'ont plus rien à voir ici, un son quelconque
trouve son pareil dans un autre son à l'unisson; c'est le rapport de 1 à 1.
C'est là l'embryon de la musique ; réduite ainsi à un seul son, elle serait
vraiment trop monotone pour avoir chance de passionner les foules. Il faut donc,
chercher des éléments de variété dans d'autres sons, mais en les choisissant de
telle sorte qu'ils aient des affinités faciles à saisir avec le son original.
Si une voix d'homme chante un do
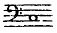 et qu'un
autre homme veuille faire comme lui, il chantera la même note; mais si c'est une
voix de femme qui veut de même en imiter l'intonation, cette note étant trop
grave pour elle, elle cherchera dans son étendue ce qui y ressemble le
plus, et trouvera le do et qu'un
autre homme veuille faire comme lui, il chantera la même note; mais si c'est une
voix de femme qui veut de même en imiter l'intonation, cette note étant trop
grave pour elle, elle cherchera dans son étendue ce qui y ressemble le
plus, et trouvera le do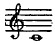 , à l'octave supérieure;
c'est, mathématiquement, le rapport de 1 à 2. , à l'octave supérieure;
c'est, mathématiquement, le rapport de 1 à 2.
Après le rapport 1: 2, le plus simple est évidemment te rapport 2 : 3. Or, si
l'on veut bien se souvenir de la série des sons harmoniques, on reconnaîtra que
ce rapport représente la quinte juste.
Il y a quelques années, étant à Pâques au Mont-Saint-Michel, j'entendais les
paysans chanter sans aucun accompagnement la Prose que tout le monde connaît : o
filii et filiæ; les basses disaient gravement :
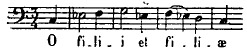 ; ;
les voix des femmes et des enfants les accompagnaient à l'octave :
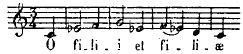 , ,
tandis que les femmes âgées et les jeunes garçons dans la mue, gênés par
ces registres trop hauts ou trop graves pour eux, prenaient bravement un moyen
terme, à la quinte des basses et à la
quarte des dessus :
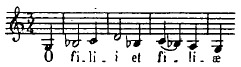
Le résultat était atroce pour mes oreilles :
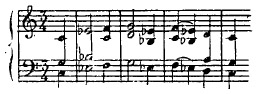
Au moyen âge, il eût paru satisfaisant et correct. Il dérive, en effet, d'une loi
parfaitement vraie et naturelle; après le rapport 1: 2, qui est l'octave, les
plus simples sont 2 : 3, qui est la quinte, et 3 : 4, qui est la quarte,
et les paysans en question agissaient d'une façon entièrement logique, mais
primitive.

Il est donc avant tout nécessaire d'admettre et de comprendre qu'aussi bien
mathématiquement que physiologiquement, il existe une grande analogie entre les
sons placés à distance d'octave, de quinte et de quarte, une ressemblance telle
que des oreilles incultes peuvent les prendre et les prennent facilement l'un
pour l'autre.
Ce qui ressemble le plus à do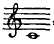 , c'est d'abord do
, c'est d'abord do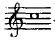 puis ensuite sol puis ensuite sol
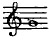 ; donc, un individu peu
exercé musicalement peut jusqu'à un certain point confondre ces trois sons, et
la théorie mathématique excuse cette erreur de la manière la plus naturelle en
démontrant que les rapports qui existent entre eux sont les plus simples qui
puissent exister. Il suffit de se reporter à l'échelle d'harmoniques que nous
avons précédemment établie par le calcul et vérifiée par l'expérience sur le
monocorde pour le constater : ; donc, un individu peu
exercé musicalement peut jusqu'à un certain point confondre ces trois sons, et
la théorie mathématique excuse cette erreur de la manière la plus naturelle en
démontrant que les rapports qui existent entre eux sont les plus simples qui
puissent exister. Il suffit de se reporter à l'échelle d'harmoniques que nous
avons précédemment établie par le calcul et vérifiée par l'expérience sur le
monocorde pour le constater :
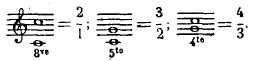
Ces trois intervalles, l'octave, la quinte et la quarte, ont donc été, dans tous
les pays, comme je l'ai déjà dit, la base de toute gamme rudimentaire, les
premiers qu'on ait pu être amené à découvrir, même sans les chercher, avec la
simple intention d'imiter un son primitif, et les
premiers par conséquent que l'on ait songé à associer et à combiner de diverses
façons, parce qu'ils étaient les plus faciles à saisir et à comparer entre eux.
Ceci bien établi, plaçons ces trois intervalles sur une même note (que nous
appelons toujours do pour la commodité du raisonnement),
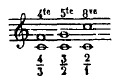
et il va devenir très simple, sans faire usage d'autres théories que celles que
nous connaissons déjà, d'expliquer la formation de la gamme diatonique, majeure
et mineure, puis, par extension, celle de la gamme chromatique.
|

