|
Accueil de la bibliothèque > La musique et les musiciens
LA MUSIQUE ET LES MUSICIENS - CHAPITRE PREMIER - Étude du son musical - Rapports des sons successifs. Tonalité. - Rapports numériques > CHAPITRE PREMIER - Étude du son musical > Rapports des sons successifs. Tonalité. - Rapports numériques Il y a plusieurs manières de se rendre compte des rapports numériques des sons
de la gamme. J'indique ici celle qui me paraît la plus simple.
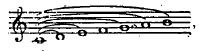
Reprenons d'abord la série des harmoniques, en la poussant, cette fois, plus
loin que nous ne l'avons fait précédemment, jusqu'au quinzième; c'est nécessaire
pour que ce tableau contienne, au moins une fois, chacun des intervalles que
nous avons à mesurer. La voici :
Or, la gamme majeure est formée de sept sons :
 , plus l'octave :
 :, et ce
sont les rapports existant entre ces sons qu'il s'agit d'établir.
Les deux premiers (do-ré), forment ce que les musiciens appellent une
seconde majeure; un intervalle semblable se trouve dans la série des
harmoniques, entre les sons 8 et 9 (do-ré). Si l'on n'a pas oublié que le numéro d'ordre des
harmoniques exprime exactement leur nombre de vibrations relativement au son
principal, et par conséquent aussi entre eux, on concevra aisément que, pendant
que do (8) fait 8 vibrations, ré (9) en fait 9; donc, pendant que
do n'en fait
qu'une seule, ré en fera une plus un huitième, c'est-à-dire 9/8. Le
rapport existant entre ces deux notes, ou tous autres sons formant une seconde
majeure, s'exprime donc par 9/8.
Le même raisonnement s'applique à tous les intervalles; nous allons l'abréger.
La tierce majeure (do-mi, 1er et 3e degrés de la
gamme) figure dans la série des harmoniques sous les numéros 4 et 5 (do-mi), ce qui veut dire que si
do est
produit par 4 vibrations, mi en exige 5; si do n'en fait qu'une (4/4), mi en devra alors faire
4/4 + 1/4 = 5/4. Le rapport 5/4 représente donc la tierce majeure.
Les harmoniques 3 et 4 (sol-do) nous donnent un exemple de quarte juste, et nous
apprennent que cet intervalle est formé par deux sons dans le rapport 3 : 4; il
en est nécessairement de même de toute autre quarte juste, et celle qui existe
entre le 1er et le 4e degré de la gamme (do-fa) sera donc bien exprimée par la fraction
4/3.
La quinte juste (do-sol, 1er et 5e degrés) est représentée dans l'échelle des
harmoniques par les sons numéros 2 et
3; donc, son rapport est 3/2.
Les sons 3 et 5 (sol-mi) nous fournissent une sixte majeure; le rapport de la
sixte majeure que contient la
gamme du 1er degré au 6e (do-la) est par conséquent
5/3.
Enfin, et c'est pour cela que nous avons étendu la série d'harmoniques, du 8e au
15e se trouve la septième majeure (do-si), la même que présente la gamme du 1er
au 7e degré, et dont le rapport est déterminé par 15/8.
L'octave, donnée par les sons 1 et 2, est formée, nous le savons depuis
longtemps, par deux sons dont l'un exécute une vibration, tandis que l'autre en
exécute deux : 2/1 = 2
Résumons tous ces rapports en un tableau :
On peut également représenter ces rapports en nombres entiers, en multipliant le
tout par 24, qui est le plus petit multiple commun des dénominateurs 2, 3, 4, 8;
on obtient ainsi le nombre relatif de vibrations pour chaque son d'une gamme
majeure parfaitement juste :
| 
