C'est ce qu'on appelle en mécanique la superposition des petits mouvements. Au moment de la rencontre de deux ou plusieurs systèmes d'ondes, les pulsations s'ajoutent les unes aux autres, s'additionnent algébriquement; mais la série alternative de condensations et de dilatations se transmet fidèlement de molécule à molécule, jusqu'à épuisement de la force initiale.

C'est ainsi qu'on peut s'instruire en faisant des ronds dans l'eau, et c'est ainsi aussi qu'on peut se représenter l'atmosphère d'une salle de concert, sillonnée en tous sens par des ondes régulières se rencontrant et s'entrecoupant en tout sens, sans que jamais aucune d'elles perde, à tous ces contacts, son individualité propre.

Mais avec cette différence que les ondes sonores donnent lieu à des combinaisons autrement compliquées que les ondes liquides et superficielles que nous venons de décrire. L'ébranlement causé par un corps qui tombe dans l'eau ne s'y manifeste d'une façon visible qu'à l'intersection de l'air et de l'eau, et les ondulations auxquelles il donne naissance se meuvent toutes dans ce même plan horizontal; c'est pourquoi nous les avons appelées des ondes circulaires. Les ondes sonores, se produisant au sein de l'atmosphère, se répandent symétriquement dans tous les sens, aussi bien en haut et en bas qu'à droite ou à gauche, tout autour enfin du corps sonore dont elles émanent; ce sont des ondes sphériques. La déperdition de force est donc en raison directe du carré de la distance qui sépare l'auditeur de la cause première du son; autrement dit, l'intensité décroît en proportion de la massa d'air ébranlée.

En plein air, par un temps calme, un son entendu à la distance de deux mètres est déjà quatre fois plus faible que si on avait l'instrument à l'oreille; à trois mètres, neuf fois; à quatre mètres, seize fois. (C'est ce que démontre la théorie mathématique ; mais dans la pratique on verra que certains sons sont doués d'une plus grande portée que d'autres, d'une plus grande pénétration, ce qui doit tenir à la présence d'harmoniques élevés, qui rendent leur timbre perçant.)

Si, par un moyen quelconque, on évite la diffusion latérale des ondes sonores, on augmente dans des proportions considérables la portée du son; dans les tuyaux vides des conduites d'eau de la ville de Paris, le célèbre physicien Biot a constaté qu'en parlant a voix basse on pouvait s'entendre à plus d'un kilomètre. M. Regnault a trouvé que les ondes se propagent plus loin dans les tuyaux d'un fort diamètre que dans ceux de section étroite, ce qui prouve qu'une partie de la force s'use sur les parois du tuyau.

Un coup de pistolet chargé d'un gramme de poudre s'entend à 1,159 mètres dans un tuyau dont le diamètre est 0^m,108; dans un tuyau de 0^m,300, il porte jusqu'à 3,810mètres; enfin, si ce tuyau a 1^m,100; ce même bruit est encore perceptible à 9,540 mètres. C'est sur ce principe que sont construits les tuyaux acoustiques.

Mais il y a d'autres moyens de diriger les ondes sonores. Tout comme les rayons lumineux, les rayons sonores jouissent de la propriété d'être réfléchis et réfractés; le mur auquel est adossé un orchestre et les voûtes du plafond constituent pour le son de véritables miroirs. Le son se reflète sur une surface polie exactement comme la lumière, et pour lui, aussi bien que pour elle, l'angle d'incidence est égal à l'angle de réflexion.

Le son le plus faible d'un diapason, ou même le tic tac d'une montre, placés à l'un des foyers d'un réflecteur elliptique, convergent vers l'autre foyer, où ils sont perçus nettement. Remplacez le réflecteur elliptique par un autre de forme parabolique, et tous les rayons seront renvoyés parallèlement, selon l'axe de la parabole. Tout naturellement, un son peut subir plusieurs réflexions successives sur des parois disposées convenablement, agissant sur lui comme un jeu de glaces agit sur
la lumière. C'est à cette propriété que sont dus les échos, dont nous parlerons plus loin, ainsi que le roulement du tonnerre, au moins en grande partie; dans ce dernier cas, les nuages constituent des surfaces réfléchissantes.

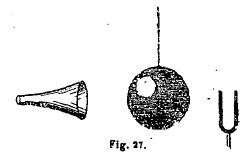Le son peut également être réfracté en traversant des milieux d'inégale densité, et, bien que cette propriété n'ait reçu jusqu'à présent aucune application artistique, nous allons décrire un moyen facile de s'en assurer : à quelques centimètres d'un diapason vibrant suspendez un ballon de baudruche dans lequel vous aurez introduit du gaz acide carbonique, plus dense que l'air; éloignez-vous graduellement jusqu'à un mètre ou un mètre cinquante, en tenant près de l'oreille un entonnoir formant cornet acoustique (fig. 27). Vous trouverez aisément dans ces parages un point où le son du diapason atteindra un maximum d'intensité; à ce moment, faites remplacer le diapason par une montre, et vous en percevrez tous les bruits aussi distinctement que si vous la teniez près de l'oreille. Le ballon aura fait converger les rayons sonores comme une lentille de verre aurait fait converger les rayons lumineux.

Cet effet est dû à la différence d'élasticité et de densité qui existe entre le gaz acide carbonique et l'air atmosphérique. La réfraction des rayons est un effet du ralentissement de leur marche dans l'épaisseur du ballon.